Measures of Association in SPSS 10
This crosstabs table
below relates two discrete, ordinal variables
- The dependent variable
is "Party ID" -- a seven scale ranging from 0 to 6 in the
2000 NES survey
- The independent variable
is "liberal-conservative" ideology -- a seven-point scale
ranging from 1 to 7
- The two variables are
obviously related; what's the appropriate measure of
relationship?
|
Crosstabulation
-- K1x. PARTY ID SUMMARY by R's placement on
Liberal-Conservative scale
|
|
|
R's placement on
Liberal-Conservative scale
|
Total
|
|
K1x.
PARTY ID SUMMARY
|
extremely
liberal
|
liberal
|
slightly
liberal
|
moderate
|
slightly
conservative
|
conservative
|
extremely
conservative
|
|
|
Strong
Democrat
|
7
|
35
|
24
|
32
|
10
|
15
|
1
|
124
|
|
Weak
Democrat
|
2
|
13
|
17
|
38
|
11
|
8
|
|
89
|
|
Ind
Democrat
|
6
|
16
|
21
|
46
|
7
|
11
|
|
107
|
|
Independent
|
|
4
|
8
|
30
|
9
|
10
|
3
|
64
|
|
Ind
Republican
|
|
4
|
7
|
32
|
30
|
15
|
6
|
94
|
|
Weak
Republican
|
1
|
2
|
6
|
24
|
29
|
24
|
6
|
92
|
|
Strong
Republican
|
|
1
|
2
|
12
|
17
|
57
|
10
|
99
|
|
Total
|
16
|
75
|
85
|
214
|
113
|
140
|
26
|
669
|
SPSS Users' Guide on page 84-87 describes several
measures of association:
- The gamma
coefficient by Goodman and Kruskal
- computes the
difference between "discordant" and "concordant" ranks
among every pair of cases
- The tau-b and
tau-c coefficients by Kendall
- works much like
gamma, except that cases tied on ranks are treated
differently
- The d coefficient
by Somers
- an asymmetric
extension of gamma, in which each variable is treated
as dependent.
- The rank-order
correlation coefficient by Spearman
- uses the rank-order
of each variable in computing the Pearson product
moment correlation
- The regular
Pearson product moment correlation itself.
Here's the SPSS output from the above table, asking for
all ordinal measures

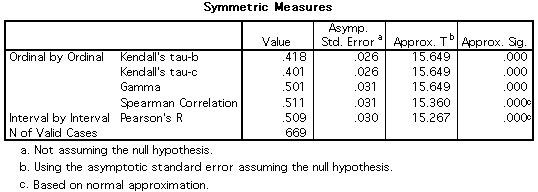
Why are there so many different measures to supplement
the Pearson correlation?
- Because all of them have
weaknesses -- which we will not cover
- It's sufficient for our
course to note that there are alternative measures
of association for ordinal data
- These measures were
created to deal with the nature of ordinal data
- The values on an
ordinal scale reflect magnitude
- But we do not know
the distances between values on an ordinal
scale
- Thus, the Pearson
correlation coefficient is
inappropriate
- We need measures
of association designed for ordinal
variables.
- But according to the
argument in Labovitz's article
- It doesn't make much
difference what the "true" distances are,
- as long as one
preserves monotonicity in scoring the
variables
- That is, match the
magnitude of the scores to the order of the
values
- Intercorrelations
among ordinal variables with widely different scoring
schemes are still high
- According to his
argument, which I endorse, just compute Pearson's
r for ordinal data.
|

