|
A problem for multiple regression
- One dependent
variable: REAGAN84 -- % vote by state for Reagan in
1984
- Three independent
variables:
- % vote for Reagan in
1980 <------ past voting history of
state
- % Black
<--------------------------- the "Jackson
factor"
- % Women
<------------------------ the "Ferraro
factor"
- Correlation
matrix: A table showing intercorrelations among
all variables
- Bivariate results
- As shown previously,
the vote for Reagan in 1980 is strongly related to the
vote for Reagan in 1984.
- The vote for Reagan
in both 1980 and 1984 is strongly correlated with %
Black and % Women -- but slightly LESS in 1984 than
1980.
- The two demographic
variables, Black and Women, are themselves highly
correlated.
- Multiple regression is
needed to assess the combined explanatory power of
all three independent variables, magically (i.e.,
statistically) adjusting for their
intercorrelations
The explanatory model underlying multiple
regression
- Here is a schematic
presentation of the simplest model of additive effects:
- Here is the regression
model expressed mathematically:
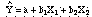
- Assumptions of this
simple additive model
- Independent variables
are not causes of each other.
- They are not caused
by other common variables.
- Therefore the
independent variables are uncorrelated.
- Departures from the
additive nature of explanation:
- In a strict additive
model, the variance explained by each variable can be
added to that explained by the other
variables.
- In practice, strict
additivity rarely obtains because independent
variables tend to be correlated.
- In practice, every
variable added to the equation will increase its power
of explanation but in decreasing amounts.
- Usually, there is
little increase after adding 5 or 6
variables.
Multiple regression as an extension of simple linear
regression
- Linear regression model
for one independent variable
- Unstandardized or
"raw" data
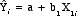
- Standardized data
(transformed into z-scores)
where  is
a standardized coefficient, not a population
parameter
- Extension of linear
model to multiple independent variables
- Unstandardized
model uses b-coefficients: Yi=
b1X1i +
b2X2i +
b3X3i+ . . . .
bnXni
- Standardized
model uses beta-coefficients:
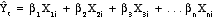
- Conceptualization
- Whereas in simple
regression, we calculated the best fitting line that
could pass through a series of points in
two-dimensional space--
- in multiple
regression, we seek the best fitting "hyperplane" that
can pass through a mass of points in k+1
dimensional space.
Computation and interpretation of
and b -- the REGRESSION COEFFICIENTS
- These values are
computed by the computer, and in practice you will not
have to calculate them yourself
- Computation of
- Relationship of
to b
- Interpretation
- b1
is the expected change in Y with one unit
change in Xi when all other variables are
controlled.
- See
the example based on the SPSS Users' Guide,
p. 198.
-
however, represents the expected change in Y in
standard deviation unitswith one standard
deviation change in Xi when the other independent
variables are controlled.
- The
b1 coefficients offer the advantage
of interpretation in the original units of
measurement
- They have the
disadvantage of making it difficult to compare the
effects of independent variables, for variables may
vary widely in means and standard deviations and thus
in their values.
- Consider the effect
of income in dollars as an independent variable
-- one unit change (i.e., $1) is likely to have a very
small effect on any Y and thus b would be
tiny.
- If measured instead
in thousands of dollars, the b
coefficient would be larger -- for one unit change
(i.e., $1,000) would have a larger effect on
Y.
-
coefficients have the advantage of being directly
comparable in relative importance of effects on Y, but
they can't be interpreted in the original measurement
scale.
Interpretation of the multiple correlation coefficient,
R
- R is the product
moment correlation between the dependent variable and the
predicted values as generated by the multiple regression
equation, using the b-coefficients.
- See
the example that illustrates the meaning of R using
data to explain female life expectancy across
nations.
- R2 as
a PRE (proportional-reduction-in-error measure of
association)
- Adjusted
R2 -- adjusting for the number of variables in
equation:
- According to the
logic of multiple regression, each new variable adds
"something" to the explanation.
- After a point, the
addition of each new variable adds less and less to
the explanation -- until the addition of a new
variable is not "worth" its contribution.
- The formula for the
"adjusted R2" allows for the number of variables
involved in the equation.
- In general, one
should not add variables beyond the point that
the adjusted R2 begins to
decrease.
where: p = number of independent variables
in equation
Assumptions of multiple regression
- Normality and
Eequality of variance for distributions of Y for
each value of the X variable (homoscedasticity,
discussed earlier)
- Independence of
observations on Y (i.e., not repeated measures on the
same unit, as in the paired samples design for the
T-Test)
- Linearity of
relationships between Y and X variables
|
