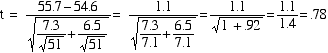The Paired Samples T-Test in Research

Usually, social researchers use the T-Test to test for significant differences between means observed for two independent groups, such as Democrats v. Republicans, or men v. women, or white v. black, and so on. These groups are independent in the sense that cases in one group are not matched with cases in the other group. But occasionally, researchers will want to determine whether there is a significant change in the scores of the same cases on the same variables over time. In this instance, the standard T-Test for Independent Samples does not apply. Consider the situation of voting turnout in American states in elections since 1980. % turnout in presidential elections by states Election N Mean Std. Deviation 1980 51 55.7 7.3 1984 51 54.6 6.5 1988 51 52.1 6.4 1992 51 57.6 7.4 1996 51 48.9 7.4 2000 51 53.8 6.9 Different stories could be told for each of these elections, but let's concentrate on the turnout data for 1980 and 1984. The 1980 election, between incumbent president Jimmy Carter and challenger Ronald Reagan also had a third candidate, John Anderson--who had been a Republican party leader but who ran as an Independent. Reagan was elected in 1980 and ran for re-election in 1984 against Walter Mondale, but there was no third party candidate in 1984. The mean voting turnout in 1984--when calculated across all the states--dropped compared with 1980. Some say that turnout dropped because there was no third party candidate. Others say that the observed differene between means of only 1.1% points (55.7-54.6) could have been attributable to chance. Perhaps we could do a standard T-Test to check this out. 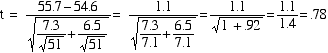Let's compute the T-Test for Independent Samples: Treating the 51 states as "Independent" in computing the T-Test produces a test statistic (t) less than one. A test statistic this small falls far short of significance at the customary .05 level, so it suggests that the observed difference in states' voting turnout between 1980 and 1984 is unlikely to have occurred by chance. But suppose that some systematic process was going on. Suppose that most states tended to demonstrate a slightly lower voting turnout rate between 1980 and 1984--perhaps dropping by about one point. Perhaps this systematic change is lost by only calculating the means for each year. In fact, because the states are matched on repeated measures, we must use the Paired Samples T-Test in SPSS, which produces this very different result: Paired Samples Statistics Mean N Std. Deviation Std. Error Mean Pair 1 % turnout in 1980 election 55.739 51 7.295 1.022 % turnout in 1984 election 54.612 51 6.541 0.916 Paired Samples Test: % turnout in 1980 election - % turnout in 1984 election Paired Differences t df Sig. (2-tailed) Mean Std. Deviation Std. Error Mean 95% Confidence Interval of the Difference Lower Upper 1.127 2.522 0.353 0.418 1.837 3.193 50 0.002 When states are matched on their turnout levels in 1980 and 1984, a paired samples T Test shows that the changes from one year to the next were small, but systematic. Such systematic shifts downward in voting turnout would have occurrred fewer than 1 time out of 100, if the shifts were purely due to change variation.