|
The nature and purpose of
analysis of variance
- Analysis of variance is
a generalization of the t-test
- The t-test is used to
test the null hypothesis: µ1
=µ2
- The t-test is
appropriate for only two groups
- Analysis of
variance, and the associated F-test, can
test for differences between any number of means for
categorized variables.
- Formally, the
null hypothesis is µ1 =
µ2 = µ3 =
µ3 ... =
µn
- Example: CLASS by grade
on 2/3 Examination in C10 Statistics
- T-Test results
for a previous class (not this year's class)
- Mean score for
undergraduates = 22.3
- Mean score for
graduates = 26.7
- T-Test showed
that this was significant far beyond the .05 level
using a one-tailed test.
- Analysis of variance
gives a general test for effect of class on
grade

-
The underlying structural model of Analysis of
variance
- Each observation in the
combined distribution represents a linear combination of
components:
Xij
= µgrand + aj + ei
j
Where:
aj = effects of group and ei
j = effects of random error
- If the treatment
or "group" effect is 0,
- then observations
will vary around the mean depending on ei
j (errors around the mean)
- these errors are
assumed to be random, normally
distributed, and sum to 0.
- This model--which
accounts for individual observations in the
distribution--can be expressed in terms of the total
variation of individual observations from the grand
mean.
- Partitioning the
total variation (also known as sum of
squares, SS):
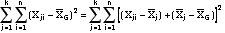
|
|
More
succinctly:
|
TSS
=
|
WSS
|
+
BSS
|
- Calculation of sums
of squares:
|

|
|
|
|
(individual score -
grand mean) = total sum of
squares
|

|
|
|
|
(individual score -
group mean) = within group sum of
squares
|
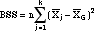
|
|
|
|
(group mean - grand
mean) = between group sum of
squares
|
An intuitive approach to what is going on:
- If the group means were
really different, then the BSS
(explained SS) would be large relative to the
WSS (unexplained SS).
- If the group means were
not much different, the WSS would be large
relative to the BSS.
The uses of BSS and
WSS
- They are measures of the
source of the total variation, and we will eventually use
them to measure the strength of the relationship between
the independent and dependent variable.
- But they have another
purpose: to test the hypothesis that the k groups are
really random samples from equivalent populations
- If they are really
drawn from the same population, then
µ1
= µ2 = µ3 =
µ4 ... = µn --
as we hypothesized
- But if they really
are drawn from equivalent populations, then
also
 1
= 1
=  2
= 2
=  3
= 3
=  4
.... 4
....  n n
- To test if they are from
equivalent populations, we actually test for equality of
estimates of population
variance.
BSS and WSS as tests of
population variance
- Each of these provide
the basis for two independent estimates of the
population variance
- One estimates the
population variance based on the variance
within each of the samples
- The other estimates
the population variance based on variance
between the sample means
- The F test is simply a
ratio between these two estimates of the
population variance:
|
F
=
|
estimate of
variance based on between mean
variation
|
|
estimate of
variance based on within group
variation
|
- If this ratio is small,
then the two estimates agree closely, and we conclude
that the groups represent random samples from equivalent
populations: i.e., same means and
variances
How do we get these
estimates of the population variances?
- They must be divided by
the appropriate degrees of freedom
- BSS / k-1 =
between groups mean square (read "mean
square" as the mean of the sum of
squares)
- WSS / N-k =
within groups mean square
SPSS ONEWAY analysis of variance for class effect on 2/3
exam (from a class in the 1990s)
ONEWAY EXAM2 BY CLASS (1,5) / STATISTICS = DESCRIPTIVES
ANALYSIS OF VARIANCE
SUM OF MEAN F F
SOURCE D.F. SQUARES SQUARES RATIO PROB.
BETWEEN GROUPS [BSS] 4 406.9775 101.7444 5.4662 .0006 <--The payoff!
WITHIN GROUPS [WSS] 84 1563.5169 18.6133
TOTAL [TSS] 88 1970.4944
STANDARD STANDARD
GROUP COUNT MEAN DEVIATION ERROR MINIMUM MAXIMUM
GRP 1 2 19.0000 14.1421 10.0000 9 29
GRP 2 13 23.1538 3.3128 .9188 17 29
GRP 3 31 22.7097 4.6918 .8427 13 31
GRP 4 16 21.3125 2.9148 .7287 17 28
GRP 5 27 26.6667 4.1324 .7953 15 32
TOTAL 89 23.6404 4.7320 .5016 9 32
|
|