Path: janda.org/c10 > Syllabus > Topics and Readings > Testing Hypotheses > Two Sample Tests
Statistical Inference:
 Two-sample Difference of Means Test
  • Independent Samples design
    • Classical design used in psychology
      • N subjects are randomly assigned to two groups.
        • Random assignment insures that individuals have an equal chance of being in either treatment group
      • After treatment, the individuals are measured on the dependent variable.
      • A test of differences in means between groups provides evidence for the treatment's effect.
      • Features of good experimental design:
        • Blind assignment
        • Blind experimenter
        • Double-blind study
    • Approximation in political and social research
      • Little potential for nor experience with experimental design.
      • Instead, social researchers tend to select out two populations (or samples) on the basis of some control variable between the two groups.
      • This is not as neat as psychologists or statisticians like, but it's what social researchers usually have to work with.
  • Related Samples design
    • The observations are not made on independent samples but on matched subjects or even the same subjects.
      • Matched-pairs design
        • Cases in both groups chosen to be similar on certain factors thought to be causes of the dependent variable.
        • Examples:
          • Individuals matched on sex, height, weight, age.
          • Nations matched on GNP, size, type of government
        • Because some sources of variation are controlled, a matched-pairs test is designed to detect smaller variations in the dependent variable -- such as expenditures for defense, in the case of nations.
      • Repeated-Measures design (paired data in SPSS)
        • Uses the same cases but takes observations before and after treatment.
        • Reduces possible variation even more.
        • In political and social research, may be used with repeated measures on the same states over time.
  • Summary:
    • If random factors only make the determination, the test for differences of means should be conducted as if the data were from independent samples.
    • If the groups are matched before the experiment or if the same subjects are used, the test of difference of means should be conducted as if the data were from related samples.
    • In political and social research, most tests for the difference between means employ independent samples.

The appropriate test for difference of means in SPSS: T-Test

  • Available under the Analyze Menu in SPSS 10
    • Choose Compare Means
    • Select Independent-Samples T Test -- if your data are divided into two unmatched groups, e.g.
      • Democrats v. Republicans
      • Men v. women
      • Undergraduates v. graduates
    • Select Paired-Samples T Test -- if your data consists of repeated measures on the same units, e.g.
      • comparing same students' performance on 1/3 and 2/3 examinations
      • comparing same states' voting turnout in 1996 and 2000 presidential elections

The conceptual model underlying both types of T-Test:

  • compare the difference of means for sample 1 with sample 2:
    • Strictly speaking, the test is for the difference computed between the means of two samples, drawn and computed an infinite number of times, compared with the difference between the two means of their parent populations:
  • But since the two population means, 1 and 2, are assumed to be equal, 1 - 2 = 0, so the second term drops out, and the test becomes simply a test for the observed difference between the sample means:
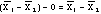
  • As in the standard "model" of hypothesis testing, this observed difference in sample means can be evaluated by dividing by some "standard error" allowable for sampling differences.
    • Assuming independent samples, the STANDARD ERROR of the sampling distribution of the DIFFERENCE IN MEANS is
       
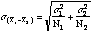
    • When 1 and 2 are known, the formula becomes
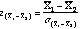
    • When 1 and 2 are estimated by sample values and where: s = unbiased estimate of , we can compute
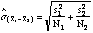
    • Thus, the formula using as an estimate of becomes
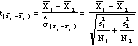
  • Using estimated values for the population variances produces the same formulate, except that when SAMPLE SIZES are SMALL (30 cases or less), the t-distribution must be used.
  • For historical reasons, the difference of means test is referred to as the t-test, even thought the t distribution is really necessary only for small samples.