Path: janda.org/c10 > Syllabus > Topics and Readings > Testing Hypotheses > Tails and Errors
Hypothesis Tests and Types of Errors
Formulating hypotheses for testing
Two types of hypotheses
 
Research hypothesis (also known as the alternative hypothesis)
The substantive hypothesis of interest we really want to test.
EXAMPLE: Northwestern students are atypical of college students in ideological attitudes, i.e, they have DIFFERENT attitudes
In saying they are different, we are not specifying that NU students are either more liberal or more conservative -- only that they are different without saying HOW MUCH or in WHAT DIRECTION.
A lack of specificity in the research hypothesis leads to the null hypothesis
We test the research hypothesis indirectly by testing the similarity between NU students and other students
The NULL hypothesis states that there is NO DIFFERENCE between the mean ideological orientation of NU students and others
Hence, it asserts that NU ideology = Population ideology
Or, expressed differently, NU ideology - Population ideology = 0
Hence, this assertion is called the NULL hypothesis, for it asserts 0 difference.
Testing the null hypothesis
Formalization:
H0 = NU - population = 0
H1 = NU - population is not = 0
If we disprove H0, we can accept H1
Consider this example:
Assume that we create a 5 point scale to measure conservatism:
 
1=far left
2=liberal
3=middle-of-road
4=conservative
5=far right
 
  • American Council on Education (ACE) Data for all entering college students in 1994 showed 2.97 as their mean score on this scale.
  • Data from a sample of 1,184 NU students show a score of 2.87, meaning the sample of NU students is more liberal than the population of all students
  • But because we have data from only a sample of NU students, it is possible that sampling error could account for the difference of .10 points on the conservatism scale and that NU students as a whole had a mean of 2.97 like the population.
  • How can we test to determine the likelihood of observing a score of 2.87 if in fact NU students as a whole did score 2.97, just like the national population? 

Testing an observed sample mean against a hypothesized population mean

This involves the Difference of Means Test-- for a "single sample"

  • Compute the mean for sample data,
  • Subtract the population mean from the sample mean, 
  • Evaluate the difference (if any) in terms of (i.e., dividing by) the standard error of the sampling distribution of means:
    • i.e., the standard deviation of a hypothetical distribution of an infinite number of sample means of size N
    • coming from a population with standard deviation, 
    • Remember:
      • the standard deviation of a sampling distribution is known as
      • the standard error of mean
      • s.e. = sigma =  
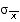
  • This formula applies, when the population standard deviation, sigma, is known.
  • What would be the likely conservatism score if we took another sample?
  • Factors in the variability of sample means:
    • The amount of ideological variation in the population of NU students.
    • The size of the sample N (but not the % the sample is of all NU students)
  • Formula for standard error of sampling distribution of means:
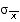
    • This formula assumes that we know the standard deviation of the attribute in the population. And we do, it is .77.
     
    Computing the standard error

s.e. of the sampling distribution of means =
.77 ÷ sqrt(1184) =

.77 ÷ 34.4 = .022
Computing the TEST STATISTIC: a z-score

z-score = (X - µ) ÷ s.e.

= (2.87 - 2.97) ÷ .022

= -.10 ÷ .022

= - 4.5

Given a normal distribution (and the sampling distribution of means distributes normally), a z-score with an absolute value of 4.5 (whether it is negative or positive) is highly unlikely. 

  • To interpret a test statistic such as z = -4.5, one needs some decision rules:
    • Set a level of significant that indicates how "deviant" or unlikely a test statistic is before we call it "significant" 
    • This level of significance is called the alpha level.
      • It refers to a chosen probability or significance level.
      • It expresses the probability of a Type I error, rejecting a true null hypothesis.
      • Convention, and not much else, often sets alpha at .05.
    • Meaning of a test statistic significant at the .05 level: such a test statistic would occur only as often as 5 times in 100 samples if in fact the population had the hypothesized mean
  • The level of significance and the alpha value are associated with the region of rejection delineated on a normal curve.
    • If a z-score is observed that falls in the region of rejection, the decision rule is to reject the null hypothesis. 
    • The z-score that marks the region of rejection is called the critical value. 
    • Thus, in essence, the test statistic (observed z-score) is compared with the critical z-score, and the decision to accept or reject the null hypothesis depends on the comparison.
       
When the population standard deviation, , is NOT known
  • This is the usual case -- we don't know EITHER µ or
  • Because we need s to compute the standard error of the mean, we must estimate , which we can call .
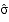  • Our best estimate, 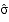, of the population standard deviation, , is the sample standard deviation, s.
    • In our case, the s.d. for 1,184 NU students was .81.
    • Recall that the population was .77.
  • Unfortunately, the formula that we have used up to now to compute the standard deviation, s, does not yield the correct estimate of the population standard deviation, , for it is a biased estimate.
    • You learned to calculate the standard deviation as
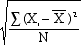
    • But when calculated that way,
      • the standard deviation for samples systematically underestimates the population standard deviation.
      • Because it is biased, we must adjust the formula by dividing the variation by N-l instead of N.

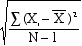
  • SPSS routinely calculates the sample standard deviation, s, to provide an unbiased estimate of the population standard deviation, .
  • This formula computes the unbiased sample standard deviation
    • which we will call s'
    • to distinguish it from s when computed with N in the formula's denominator. 
  • The standard deviation for a sample as calculated by SPSS is the corrected, unbiased estimate of the population standard deviation. 
  • This value is used to compute the estimated standard deviation of the sampling distribution of means: which is used to estimate the known value . 

When the population standard deviation is estimated, rather than known--new error enters.

  • The smaller the sample, the greater the error in estimation. 
  • The resulting test statistic no longer "distributes z" (normally) instead it "distributes t"
    • There is a different t distribution for each degree of freedom, measured by N - 1 
    • The smaller the sample, and the fewer the degrees of freedom, the flatter the t distribution -- i.e., the more spread it has 
  • When sample sizes are large (around 100), the normal and t distributions converge. 
  • Thus, when sample sizes are small and s is estimated by s', be sure to consult the t-distribution rather than the normal distribution in assessing the test statistic.