Summary Statistics: Measures of Central Tendency

Three Major Measures of Central Tendency   MODE is the most frequent value in a data distribution The mode is suitable for all types of data: NOMINAL through RATIO In practice, the mode is suitable only for variables with limited values Visual display of mode and bimodal distributions using smooth frequency polygons Unimodal: Mode Bimodal: Mode--almost the mode MEDIAN is the value that exactly divides an ordered frequency distribution into equal halves Suitable for ORDINAL variables and higher -- NOT for NOMINAL data 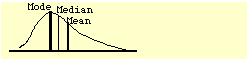Visual display of data: in a symmetrical, unimodal distribution, the mode and median are identical   MEAN Commonly known as the "average," the mean is the sum of all values divided by the number of cases: (This is your first confrontation with higher mathematics.) In a symmetrical, unimodal distribution, the mode, median, and mean will be identical.   In a unimodal but skewed distribution, the median will lie between the mode and the mean. Skewed distributions are defined by positions of their TAILS NEGATIVELY skewed distributions have their tails to the LEFT POSITIVELY skewed distributions have their tails to the RIGHT Negative skew Positive skew Consider the example of family income, which is a positively skewed distribution A few very wealthy families will skew the distribution to the right and thus raise the mean, but a few very wealthy people will have little effect on the median. Thus, the median is a preferred measure of central tendency for family income. But in general, the mean is the most important measure of central tendency in statistics -- for a technical reason: the mean is the number which has the smallest squared distance from all other numbers in the distribution. Let's study the means, medians, and modes you were asked to compute for the assigned variables, by following the usual procedure, going first to the Analyze Menu, then choosing Frequencies, which produces this dialog box, which shows that five variables were selected from list at the left, moved to the right list, and that the "Display frequency tables" box was NOT check--because these are continuous variables and the frequency tables would have little value. : The next step was to click on the statistics box above to go to this dialog box: Checking the three measures of Central Tendency--Mean, Median, and Mode--produces this result: % women population in 1989 % black population in 1990 % vote for G. W. Bush in 2000 % vote for Al Gore in 2000 % vote for Ralph Nader in 2000 N Valid 51 51 51 51 51 Missing 0 0 0 0 0 Mean 48.07 10.636 49.697 46.04 3.039 Median 47.65 7.137 50.42 46.44 2.54 Mode 48.2 0.3a 9a 47.9 0 a Multiple modes exist. The smallest value is shown How come the mean vote for G.W. Bush, who did not win a plurality of the popular vote, was higher than the mean vote for Al Gore, who won the popular vote but lost the electoral vote? This statistical curiousity illustrates what's called the ecological fallacy -- the danger of attributing the result of data analysis at one level to another level. We attributed the result of a finding at the state level to the national level. Measures of central tendency are useful, but statistics actually relies more on the other type of summary statistics: measures of dispersion (variation).