Test for the significance of relationships between two CONTINUOUS variables

• We introduced Pearson correlation as a measure of the STRENGTH of a relationship between two variables
• But any relationship should be assessed for its SIGNIFICANCE as well as its strength.

A general discussion of significance tests for relationships between two continuous variables.

• Factors in relationships between two variables
  • The strength of the relationship:
    • is indicated by the correlation coefficient: r
    • but is actually measured by the coefficient of determination: r²
  • The significance of the relationship
    • is expressed in probability levels: p (e.g., significant at p =.05)
    • This tells how unlikely a given correlation coefficient, r, will occur given no relationship in the population
      • NOTE! NOTE! NOTE! The smaller the p-level, the more significant the relationship
      • BUT! BUT! BUT! The larger the correlation, the stronger the relationship
• Consider the classical model for testing significance
  • It assumes that you have a sample of cases from a population
  • The question is whether your observed statistic for the sample is likely to be observed given some assumption of the corresponding population parameter.
  • If your observed statistic does not exactly match the population parameter, perhaps the difference is due to sampling error
  • The fundamental question: is the difference between what you observe and what you expect given the assumption of the population large enough to be significant -- to reject the assumption?
  • The greater the difference -- the more the sample statistic deviates from the population parameter -- the more significant it is
  • That is, the lessl ikely (small probability values) that the population assumption is true.
•  The classical model makes some assumptions about the population parameter:
  • Population parameters are expressed as Greek letters, while corresponding sample statistics are expressed in lower-case Roman letters:

    • r = correlation between two variables in the sample
    • (rho) = correlation between the same two variables in the population

  • A common assumption is that there is NO relationship between X and Y in the population: = 0.0
  • Under this common null hypothesis in correlational analysis: r = 0.0 

• When the test is against the null hypothesis: r _xy = 0.0
  • What is the likelihood of drawing a sample with r _xy ­ 0.0?
  • The sampling distribution of r is
    • approximately normal (but bounded at -1.0 and +1.0) when N is large
    • and distributes t when N is small.
  • The simplest formula for computing the appropriate t value to test significance of a correlation coefficient employs the t distribution:

    

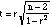
  •  The degrees of freedom for entering the t-distribution is N - 2
    
• Example: Suppose you obsserve that r= .50 between literacy rate and political stability in 10 nations
  • Is this relationship "strong"?
    • Coefficient of determination = r-squared = .25
    • Means that 25% of variance in political stability is "explained" by literacy rate
  • Is the relationship "significant"?
  • That remains to be determined using the formula above

    r = .50 and N=10

    set level of significance (assume .05)

    determine one-or two-tailed test (aim for one-tailed)

    

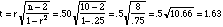
  • For 8 df and one-tailed test, critical value of t = 1.86
    • We observe only t = 1.63
    • It lies below the critical t of 1.86
    • So the null hypothesis of no relationship in the population (r = 0) cannot be rejected
       
• Comments
  • Note that a relationship can be strong and yet not significant
  • Conversely, a relationship can be weak but significant
    • The key factor is the size of the sample.
    • For small samples, it is easy to produce a strong correlation by chance and one must pay attention to signficance to keep from jumping to conclusions: i.e.,
      • rejecting a true null hypothesis,
      • which meansmaking a Type I error.
  • For large samples, it is easy to achieve significance, and one must pay attention to the strength of the correlation to determine if the relationship explains very much.
    
•  Alternative ways of testing significance of r against the null hypothesis
  • Look up the values in a table
  • Read them off the SPSS output:
    • check to see whether SPSS is making a one-tailed test
    • or a two-tailed test 

• This is a more complex procedure, which is discussed briefly in the Kirk reading
  • The test requires first transforming the sample r to a new value, Z'.
    • This test is seldom used.
    • You will not be responsible for it.