Summary Statistics: Measures of Dispersion

Various Measures of Dispersion In many ways, measures of central tendency are less useful in statistical analysis than measures of dispersion of values around the central tendency The dispersion of values within variables is especially important in social and political research because: Dispersion or "variation" in observations is what we seek to explain. Researchers want to know WHY some cases lie above average and others below average for a given variable: TURNOUT in voting: why do some states show higher rates than others? CRIMES in cities: why are there differences in crime rates? CIVIL STRIFE among countries: what accounts for differing amounts? Much of statistical explanation aims at explaining DIFFERENCES in observations -- also known as VARIATION, or the more technical term, VARIANCE.   The SPSS Guide contains only the briefest discussion of measures of dispersion on pages 23-24. It mentions the minimum and maximum values as the extremes, and it refers to the standard deviation as the "most commonly used" measure of dispersion. This is not enough, and we'll discuss several statistics used to measure variation, which differ in their importance. We'll proceed from the less important to the more important, and we'll relate the various measures to measurement theory.  Easy-to-Understand Measures of dispersion for NOMINAL and ORDINAL variables In the great scheme of things, measuring dispersion among norminal or oridinal variables is not very important. There is inconsistency in methods to measure dispersion for these variables, especially for nominal variables. Measures suitable for nominal variables (discrete, non-orderable) would also apply to discrete orderable or continuous variables, orderable, but better alternatives are available. Whenever possible, researchers try to reconceptualize nominal and ordinal variables and operationalize (measure) them with an interval scale. Variation Ratio, VR VR = l - (proportion of cases in the mode) The value of VR reflects the following logic: The larger the proportion of cases in the mode of a nominal variable, the less the variation among the cases of that variable. By subtracting the proportion of cases from 1, VR reports the dispersion among cases. This measure has an absolute lower value of 0, indicating NO variation in the data (occurs when all the cases fall into one category; hence no variation). Its maximum value approaches one as the proportion of cases inside the mode decreases. Unfortunately, this measure is a "terminal statistic": VR does not figure prominently in any subsequent procedures for statistical analysis. Nevertheless, you should learn it, for it illustrates that even nominal variables can demonstrate variation that the variation can be measured, even if somewhat awkwardly. Easy-to-understand measures of variation for CONTINUOUS variables.   RANGE: the distance between the highest and lowest values in a distribution Uses information on only the extreme values. Highly unstable as a result. SEMI-INTERQUARTILE RANGE: distance between scores at the 25th and the 75th percentiles. Also uses information on only two values, but not ones at the extremes. More stable than the range but of limited utility. AVERAGE DEVIATION: where = absolute value of the differences   Absolute values of the differences are summed, rather than the differences themselves, for summing the positive and negative values of differences in a distribution calculating from its mean always yields 0. The average deviation is simple to calculate and easily understood. But it is of limited value in statistics, for it does not figure in subsequent statistical analysis. For mathematical reasons, statistical procedures are based on measures of dispersion that use SQUARED deviations from the mean rather than absolute deviations.    Hard-to-understand measures of variation for CONTINUOUS variables.  SUM OF SQUARES is the sum of the squared deviations of observations from the mean of the distribution. 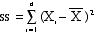The SUM OF SQUARES is commonly represented as SS The formula is This quantity is also known as the VARIATION. It appears in the numerator of formulas for standard deviation and variance (below). We will see later that this value is useful on its own. 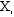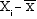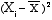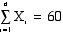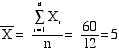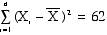Here is a "worksheet" for comuting the SUM OF SQUARES: Values of Xi (1) Deviations of Xi from the mean (2) Deviations squared (3) 5 0 0 9 4 16 2 -3 9 8 3 9 6 1 1 5 0 0 4 -1 1 7 2 4 4 -1 1 3 -2 4 1 -4 16 6 1 1 Sum of the Squared Deviations VARIANCE is simply the mean of these squared and summed deviations (i.e., the average of the squared deviations) The symbol for VARIANCE is s2 accompanied by a subscript for the corresponding variable. 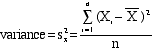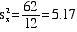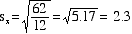Here's the formula for variance of variable X: For the data above, the variance computes as STANDARD DEVIATION, is the square root of the variance The symbol for STANDARD DEVIATION (often shortened to STD DEV) is s The formula for the standard deviation of variable X: For the data above, the standard deviation computes as  This is the most important formula in statistics But read on page 24 of the SPSS Guide that "for theoretical reasons" (n-1) is used in the demoninator to compute the standard devation, not n. Indeed, SPSS routinely uses n-1 and not n when it computes the standard deviation. But for now, learn this formula as the definition of the standard deviation. We will get to the "theoretical reasons" later.   Dispersion and the Normal Distribution Occasionally in lecture I spoke about the "shape" of a distribution of values, using these terms: unimodal -- the distribution had only a single value that occurred most frequently symmetrical -- the left side of the distribution of values mirrored the right side, i.e, it was neither skewed to the left, nor was it skewed to the right bell-shaped -- the frequencies of cases declined toward the extreme values in the right and left tails, so that the distribution had the appearance of a "bell." When such a "bell-shaped" distribution demonstrates certain properties, it is said to have a normal distribution. In one sense, it is called "normal" because a unimodal, symmetrical, bell-shaped distribution "normally" develops in the long run through accidents of nature when the events are equally-likely to occur. In an infinite amount of time, a random process could ultimately generate any structured result: e.g., a group of monkeys seated at typewriters could peck out all the great works of literature. This would be an extremely rare event, but it is conceivable. The normal curve is a mathematical formula that assigns probabilities to the occurrence of rare events. Statistically speaking, it is a probability distribution for a continuous random variable: The ordinate represents the probability density for the occurrence of a value. The baseline represents the values. The exact shape of the curve is given by a complicated formula that you do NOT need to know. The area under the curve is interpreted as representing all occurrences of the variable, X. We can consider the area as representing 100 PERCENT of the occurrences; in PROPORTIONS this is expressed as 1.0. We can then interpret AREAS under the curve as representing certain PROPORTIONS of occurrences or "probabilities". We cannot assign a probability to any point, but we can attach probabilities to INTERVALS on the baseline associated with AREAS under the curve: e.g., the mean has 50% of the cases standing to each side. Special properties of the normal distribution: Its shape is such that it Embraces 68.26% of the cases within 1 s.d. around the mean. Embraces 95.46% of the cases within 2 s.d. around the mean. Embraces 99.74% of the cases within 3 s.d. around the mean. More roughly speaking, 68%, 95%, and 99% of the cases are embraced within 1, 2, and 3 standard deviations from the mean in a normal distribution. Determining whether a distribution is "normal" The "Eyeball" test that we discussed earlier: Is the distribution unimodal? Is the distribution symmetrical? More exacting mathematical tests: measured according to "moments" or "deviations" from the mean First, the meaning of "moment" -- in physics, it is the distance or deviation from a reference point. In statistics, a "moment" is a deviation from the mean. If deviations are raised to powers of 1, 2, 3, and 4--"moments" of 1, 2, 3, and 4 are created. FIRST MOMENT: = 0 <----you know this already SECOND MOMENT: = variance <--- you had this The third and fourth moments yeild measures of fit to a normal distribution: The SPSS Guide on pages 27-28 mentions two terms, skewness, and kurtosis, which are proposed as measures of the conformity with (or departure from) a "normal distribution." skewness measures the "symmetry" of a distribution kurtosis measures the "peakedness" of a distribution THIRD MOMENT: = skewness This formula is calculated within SPSS Positive values (greater than 0) indicate right-skew (negative value, a left-skew) FOURTH MOMENT: - 3 = kurtosis Positive values signal a more peaked distribution (leptokurdic) than the normal curve Negative values indicate a flatter distribution (platykurdic)   If skewness and kurtosis values tend toward 0, then the distribution approximates a normal distribution. Suppose the distribution is not normal? No matter how the original observations are distributed, the mean plus or minus two standard deviations will include at least 75% of the observations. No matter how the original observations are distributed, the mean plus or minus three standard deviations witll include 89% or more. Assignment for today: Compute measures of dispersion for pctwomen, pctblack, and bush2000. Which is closest to a "normal distribution"?

Transforming variables to approach a normal distribution The SPSS Guide, page 27, discusses a method to transform a heavily skewed variable so that it distributes more "normally." The aim is to change its underlying scale of measurement so that large values count for less. The method described (there are others) involves taking not the absolute value of the observation but the logarithm (base 10) of the value. The chart on page illustrates how countries like China and India tend to skew the distribution of the population variable when population is measured in thousands. When population is measured as the log of the population, the variable approaches a normal distribution. The transformation reduces the extreme impact of countries with very large populations (like China and Indis) in statistical analyses that involve population as a variable. You'll understand the importance of this later. Obviously, this simple method of transformation works only for variables that are right-skewed. Fortunately, that accounts for most variables of interest to social scientists. Fortunately also, there are other techniques for transforming left-skewed variables, if that's needed.